什么是感知机
定义:假设输入空间(特征空间)$X \subseteq R^n$,输出空间是$Y={-1,+1}$,输入$x \in X$,表示实例的特征向量,对于输入空间(特征空间)中的点,输出$y \in Y$是表示实例的类别。由输入空间到输出空间的如下函数,$f(x)=sign(w \cdot x +b)$称为感知机,其中$w$和$b$称为感知机的参数。$sign$函数如下。
$$sign(x)=\begin{cases} +1, & x>=0\\-1, & x<0 \end{cases}$$
感知机数学原理
线性可分
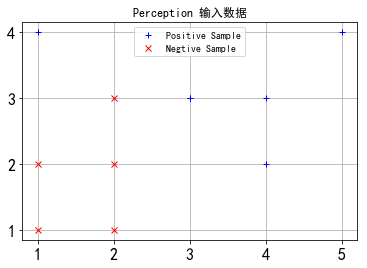
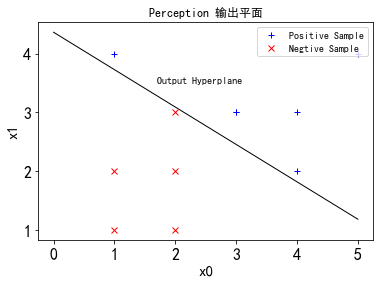
对于给定的一个数据集$T={(x_1,y_1),(x_2,y_2),…(x_n,y_n)}$,其中,$x_i \in X \subseteq R^n , y \in Y={-1, +1}, i=1,2,…,N$,如果存在某个超平面$S: w \cdot x+b = 0$,能将正负样例分到$S$两侧,则说明数据集$T$是线性可分的,那么接下来就是要求这个超平面$S$的表达式。
损失函数
数据集$T$中任意一个误分类点到这个超平面$S$的距离之和为:
$$\frac{1}{\Vert w \Vert}\sum_{x_i \in M}{\vert w \cdot x_i+b \vert}$$
其中$M$为误分类点的集合。如何去掉绝对值呢?我们注意到$y_i$的取值是有好处的。对于误分类点来说$y_i$的符号和$w \cdot x_i+b$相反。且$y_i$取值+1,-1。则我们可以将上式转换成:
$$- \frac{1}{\Vert w \Vert}\sum_{x_i \in M}{y_i (w \cdot x_i+b)}$$
确定损失函数时,不考虑$\frac{1}{\Vert w \Vert}$。
- Q:感知机损失函数确定过程中的系数$\frac{1}{\Vert w \Vert}$,为什么可以忽略?
- 1)感知机的损失函数时基于误分类的,$L2$范数项不会影响$y_i (w \cdot x_i+b)$的正负判断,所以$\frac{1}{\Vert w \Vert}$对感知机学习算法的中间过程可有可无
- 2)$\frac{1}{\Vert w \Vert}$不影响感知机学习算法的最终结果,当所有输入被正确分类时,不存在误分类的点,此时损失函数为零,缺少此项并不会影响感知机损失函数的收敛
- 3)我思考的是即使缺少这个项,损失函数也能对线性可分数据在有限次学习后正确分开。李航书上有证明。
- 4)权重$w$是一个向量,$\frac{1}{\Vert w \Vert}$的大小不会影响向量的方向,确定超平面是通过确定法向量$w$和截距$b$来确定的,而的大对权重$w$的方向没有任何影响,所以可以固定$\frac{1}{\Vert w \Vert}$|为1或者不考虑。
算法步骤
输入:训练数据$T={(x_1,y_1),(x_2,y_2),…(x_n,y_n)}$,其中,$x_i \in X \subseteq R^n , y \in Y={-1, +1}, i=1,2,…,N$,;学习率$\eta(0<\eta<=1)$;
输出:$w,b$;感知机模型$f(x)=sign(w \cdot x+b)$。
- 1)选取初值$w_0,b_0$
- 2)在训练集中选取数据$(x_i,y_i)$
- 3)如果$y_i (w \cdot x_i+b)<0$,$w \leftarrow w+ \eta y_ix_i;b \leftarrow b+ \eta y_i $
- 4)转至 2),直至训练集中没有误分类点
代码实现
1 | #初始化 |
1 | #感知机算法 |
- 李航,《统计学习方法》
- Hexo中如何配置mathjax
- Hexo中如何输入跨行公式
- Hexo无法加载本地图片
